Research of the Neumann Group
Molecular Simulation
There are various philosophies under which computer simulations (i.e. molecular dynamics and Monte Carlo methods) may be employed in Statistical Physics: For the theoretician concerned with approximation methods, they may simply be a convenient tool for obtaining reference data, providing exact numerical results for selected model systems against which predictions can be tested. At a more fundamental level, they have revolutionized our understanding of molecular processes by allowing us to study quite complex systems in full microscopic detail, thereby obtaining information that may not be accessible experimentally. Finally, and most important from a practical point of view, simulations are increasingly often used to predict the properties of real substances, or to extrapolate them to conditions where laboratory experiments are difficult or even impossible.
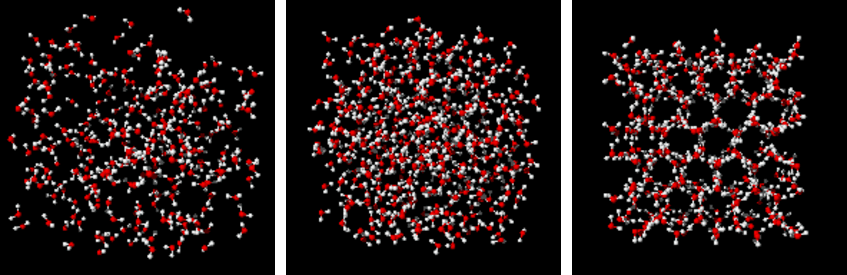
Typical snapshots from Monte Carlo simulations of compressed supercritical steam (left), liquid water at ambient conditions (center), and hexagonal ice near the melting point (right).
It was largely the latter aspect, under which our work on water and aqueous systems has been performed over the past few years. Water is not only of considerable interest as a pure substance, because of its unusual properties such as the volume increase on melting, the density maximum at 4oC, or its high dielectric constant, it also forms the ubiquitous solvent in virtually all biological and many technologically important processes. Here, in addition to the classical role of water and steam in the power generation industry, it is primarily the rapidly developing fields of geothermal solutions (geochemistry, oil production) and hydrothermal oxidation (toxic waste disposal) that require accurate knowledge of the thermophysical properties of water in a range of temperatures and densities where this substance can become extremely aggressive.

Dielectric equation of state for the SPC/E model of water; six-parameter correlation based on ca 100 Monte Carlo simulations.
The most important properties of water as a solvent are its dielectric constant and the ion product. In simulations the calculation of both is intimately connected with a correct treatment of the long-range electrostatic interactions.
Having laid the methodological ground work for this in the 1980's and demonstrated the principal feasibility of calculating the dielectric constant of water by simulation, we have since then performed quite a large number of simulations of water over a wide density and temperature range, using newly developed simple, yet highly effective methods of handling the electrostatic interactions. As a result, the "dielectric equation of state" for a few selected models of water is now available in the form of a correlation.
Hemodynamics and Visualization
Although hydrodynamics is usually regarded as part of physics, several of the pioneers in this field such as Poiseuille and Euler were originally interested in a phenomenon one would rather associate with medicine or physiology, namely the flow of blood through blood vessels. Therefore it is hardly surprising that also today similar problems are among the most important applications of numerical simulation thechniques.
Certainly the most important and interesting example is the coronary circulation, for in this system the flow patterns are not simply determined by the pressure drop between the aortic root and the right atrium, but to an even larger extent by the fact that most of the blood vessels are buried within the myocardium. Due to the pumping mechanism these vessels are periodically contracted by the surrounding muscle, thereby increasing their resistance, so that one is tempted to say that the heart is impeding its own perfusion. Obviously, a successful modeling of these complex phenomena, apart from requiring a detailed knowledge of the underlying structure of the coronary vascular tree, must also account for the vessels' elastic properties, as well as for the spatial and temporal variation of the intramyocardial pressure.
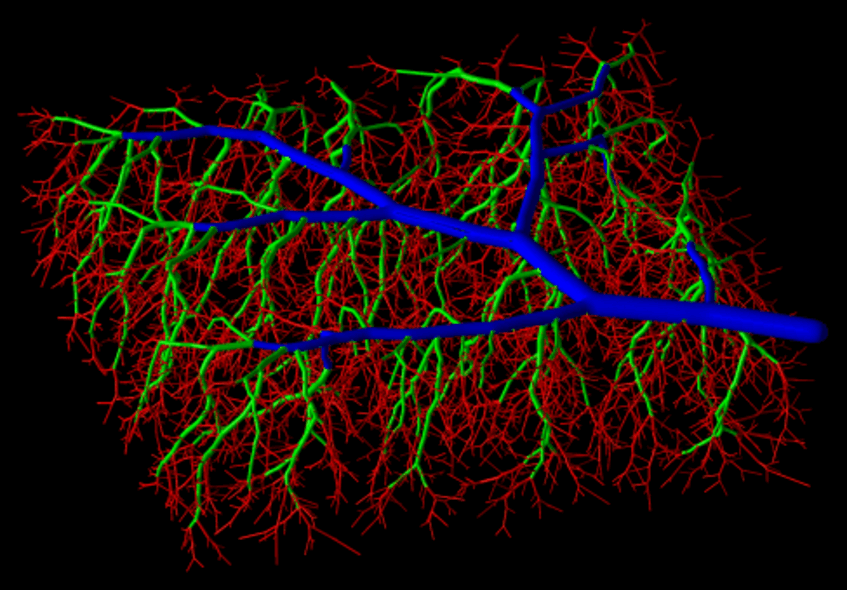
Computer-generated arterial tree supplying a slab-shaped piece of tissue, visualized as a single isosurface of a pseudopotential. Vessels belonging to different classes of radii are indicated by color coding. Here, the tree was grown in such a way that large, blood conveying vessels remain on the surface and only smaller vessels are allowed to penetrate into the perfusion volume, as would be appropriate for a model of the myocardium.
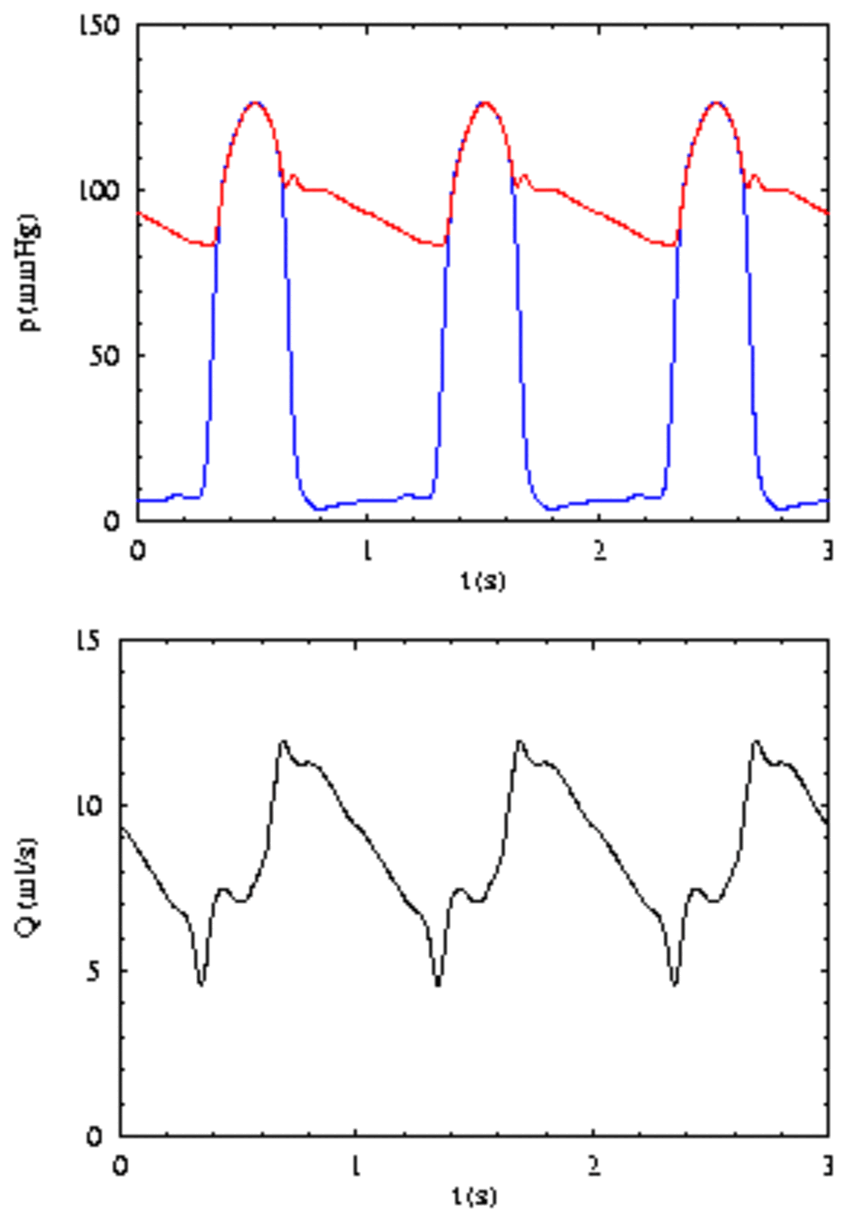
It is the interplay between the driving aortic pressure (red; top part of figure) and the opposing intramyocardial pressure (blue; here taken to be equal to the left ventricular pressure) which leads to the typical waveform observed for the total coronary inflow (bottom). Results from a hemodynamic simulation based on a vascular model similar to that shown in the preceding figure; three heartbeats at 60 bpm are shown.
The Working Group for Biomedical Computer Simulation (based at the Institute of Medical Informatics) is developing such a detailed model of coronary hemodynamics. The model is based on vascular structures generated by means of "Constrained Constructive Optimization", an optimizing stochastic growth strategy incorporating the kind of constraints required by the application. Provided that suitable parameters are chosen, the resulting structures are very similar to corrosion casts of real coronary vascular trees.
In order to visualize these computer-generated structures and to be able to highlight various properties by color coding, a specific algorithm has been developed in which the visual appearance of an entire vascular tree is defined by the isosurface of a pseudopotential which is rendered in a photorealistic way.
At present we are able to generate vascular trees comprising a few 104 individual segments. Although this is several orders of magnitude less than the actual number of vessels in an organ such as the heart, a model as detailed as that is already too complicated to be tackled by fully three-dimensional hydrodynamic methods. Therefore, the actual hemodynamic simulations are based either on the reduced one-dimensional hydrodynamic equations or on an "equivalent" nonlinear electric network. Except for the very largest vessels this is a reasonable approximation.
Currently, the elastic properties of vessels of various sizes are described by means of an extrapolation of the few available experimental data. A physiologically better founded model of vascular properties and, above all, the representation of the microcirculation and the venous part of the coronary vascular tree are the focus of the present research.
